Research

Clustering of compact objects



Globular clusters as dynamically active environments

Globular cluster NGC 6397. Image credits: D. Verschatse (Antilhue Observatory, Chile). Globular clusters (GCs) are some of the most dynamically active environments in the Universe. These spherical, dense clusters contain stars that are tightly packed, with the densest GCs having inner densities up to a million times greater than our solar neighborhood. In these environments, stellar evolution is influenced by internal dynamics, leading to phenomena like runaway mergers and mass segregation. This process pushes more massive stars closer to the center while less massive stars drift outward. As a result, GCs serve as excellent laboratories for studying compact objects such as white dwarfs, neutron stars, stellar-mass black holes, and intermediate-mass black holes (IMBHs).



Mass-modeling

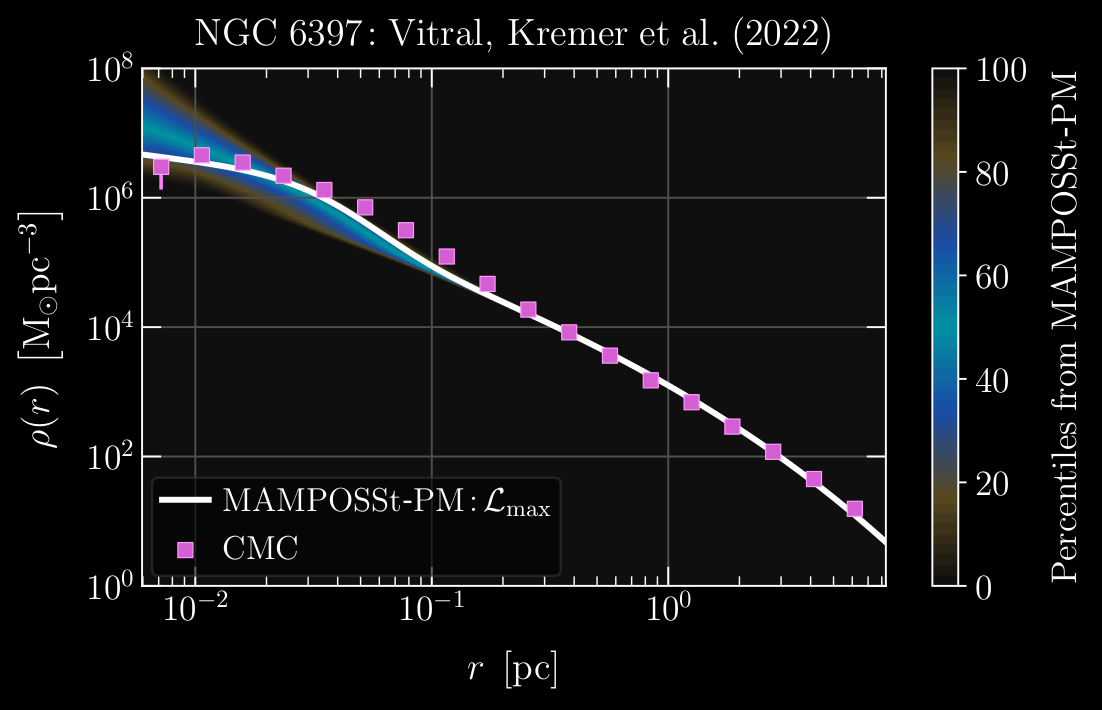Comparison of mass density profiles: The white line depicts the best fit of observed data by MAMPOSSt-PM, while the magenta squares show the respective values from the CMC model of NGC 6397. The remarkable match between the fits from observed data and simulations attest the robustness of both mass-modeling tools. Image credits: Data from Vitral et al. 2022.
Two key questions in these dense systems are: “How is mass distributed?” and “What types of stars or compact objects contribute to the cluster’s mass at various radii?” Studies suggest that excess mass in GCs may hint at the presence of intermediate-mass black holes (IMBHs), a long-sought missing link in black hole physics. To explore these questions, I employ the Jeans equation and the MAMPOSSt-PM modeling code to constrain the mass and velocity anisotropy profiles of GCs: $$\frac{{\rm d}\left (\rho\sigma_r^2\right)}{{\rm d}r} + 2\,\frac{\beta(r)}{ r}\,\rho(r)\sigma_r^2(r) = -\rho(r) \frac{G\,M(r)}{r^2} \ .$$ However, the Jeans equation alone cannot determine the stellar composition of the mass profile. To assess whether the measured mass consists of luminous stars, black holes, white dwarfs, or neutron stars, we require additional tools. Together with my collaborators, we utilize evolutionary Monte Carlo simulations from the CMC catalog, matched to Milky Way clusters. By identifying good matches, we can fully constrain the shape and composition of the mass profile in the analyzed GC.

One of the important results of my work was to show that the inner mass excess in some GCs is extended, and not point-like, as expected in the case of an IMBH. This points to the presence of an inner sub-cluster of faint compact objects.



The role of core-collapse

One of the most interesting phenomena related to GCs is the process of core-collapse, which is intrinsically related to the exchange of energy due to dynamical interactions in the cluster. In self-gravitating systems like GCs, the virial theorem reveals that the centers of GCs have a negative heat capacity, i.e. an energy input in the system triggers a decrease of the kinetic energy, which can be regarded as the system’s ‘temperature’. Such a counterintuitive relation tends to evolve in a typical cluster’s interior, as it exchanges energy with its outer regions, naturally from the former to the latter. This process leads inevitably to the ‘collapse’ of stars to the cluster’s inner-most regions.

Many works argue that core-collapse can be halted due to a process called binary burning, where dynamical interactions of binaries with other stars cause tight (‘hard’) binaries to harden while the third star (not necessarily the original one) is kicked out at a higher speed than the initial third star came in with. This process effectively pumps energy to the cluster’s inner regions, thus preventing core-collapse from continuing indefinitely.

Black holes in GCs form and sink early (on roughly 100 Myr time-scales) to the cluster’s center due to a combination of their high masses and energy equipartition. Once in the inner regions of GCs, black holes dynamically interact with one another and with luminous stars. Those living in hard binaries thus provide a similar energy exchange towards the cluster’s interior as in the classical stellar binary-burning scenario, but amplified due to the relative high masses of black holes compared to stars. This new theoretical comprehension of the physics governing GCs suggests that the ones without the characteristic inner cuspy structure of core-collapse probably harbour a segregated black hole population, responsible for the delay of core-collapse. This phenomenon has been referred to as black hole binary burning.

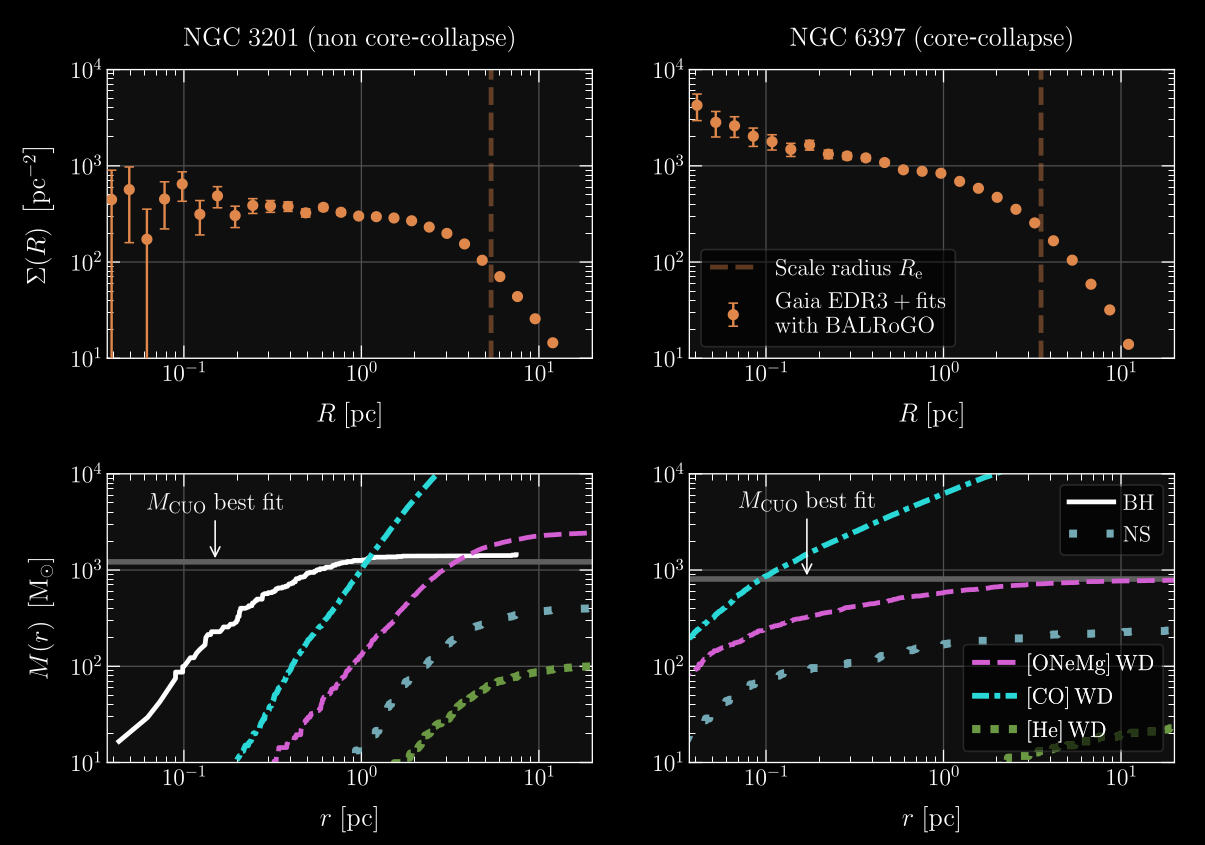The effects of core-collapse: Comparison between NGC 3201 (left), a cluster which has not yet experienced core-collapse, and NGC 6397 (right), a classic example of a cluster in a post core-collapse state. The upper panels display the surface density profiles of both clusters, from Gaia EDR3, using the same range of absolute magnitudes. The lower panels show the contribution in mass from each compact object (remnant) as a function of the 3D distance from the cluster’s centre, obtained from CMC models from Kremer et al. (2019, 2021), in addition to a grey line depicting our best MAMPOSSt-PM mass fit of a subcluster of unseen objects (i.e. MCUO). This illustrates that a collapsed population of stellar-mass black holes is a plausible explanation to the delay of core-collapse in globular clusters. The plot uses data from Vitral et al. 2022.
Ultimately (in roughly 10 Gyr timescales), the clustered black hole population becomes negligible by being ejected as the result of several dynamical interactions, allowing other luminous stellar components to sink, as well as less massive compact objects such as neutron stars and white dwarfs. When these more luminous components collapse in the centre, forming the characteristic core-collapse inner cusp, stellar and white dwarf binary-burning effectively halts further shrinking of the core.

In Vitral et al. 2022, we have confirmed that the core-collapsed GC NGC 6397 harbors hundreds of segregated massive white dwarfs (in agreement with what has been proposed by Rui et al. 2021 and Kremer et al. 2021 with simulations), by fitting data from the Hubble Space Telescope and the Gaia astrometric mission, and then matching with Monte Carlo models from the CMC catalog. In addition, by using the same methods, we constrained the black hole population in the non core-collapsed GC NGC 3201 to roughly a hundred stellar-mass black holes, concentrated in a region of roughly 0.1 parsecs.



Intermediate-mass black holes

In Vitral et al. 2023, we performed mass-anisotropy modeling of the globular cluster Messier 4 (M4), the closest of its kind to our Sun. For the first time, we fitted its 3D velocity anisotropy profile and showed it to be isotropic at the center, while tangential at the outskirts. With 2D proper motion data, we were then able to solve the mass-anisotropy degeneracy, and robustly fit the central mass profile of this cluster. We measured a dark central mass of roughly 800 ± 300 M⊙ , but it was not possible to distinguish between a point-like source, such as an intermediate-mass black hole (IMBH), and a dark population of stellar remnants of extent ≈ 0.016 pc ≃ 3300 au .

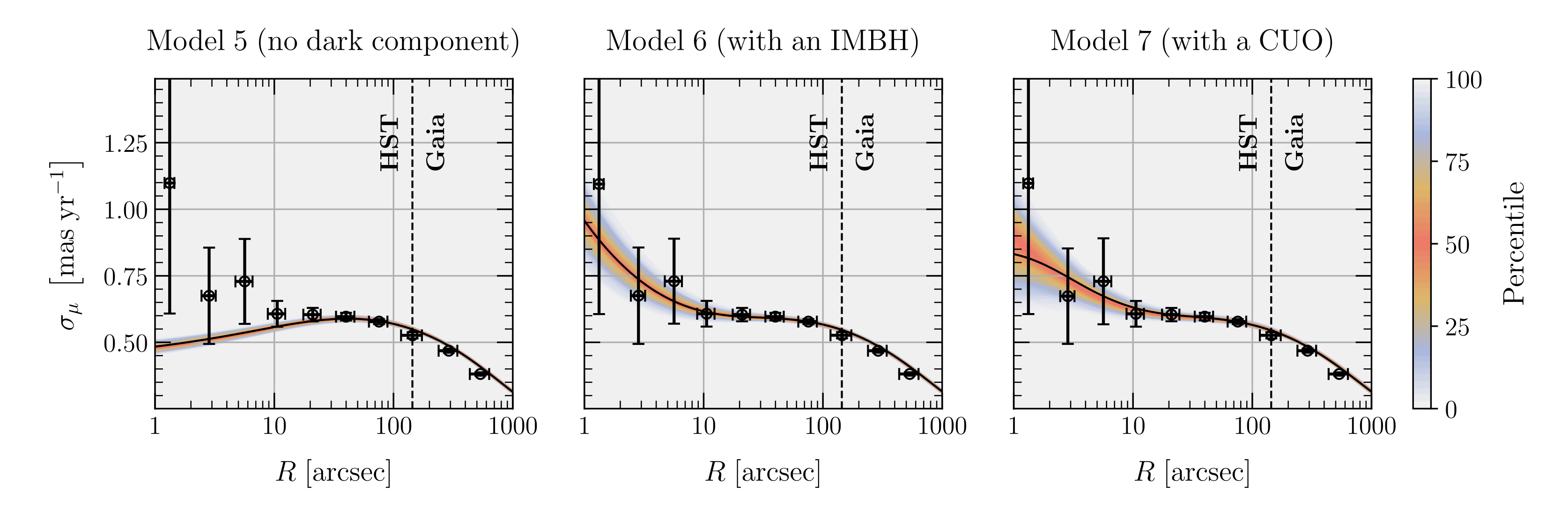Display of the proper motion velocity dispersion as a function of the projected radius of M4, for models with no dark component (left), with an IMBH (middle), and with central unresolved objects (right). The coloured regions represent the percentiles from the MCMC chains of our fit, while the continuous black solid line shows the maximum likelihood solution from MAMPOSST-PM. The black dashed line depicts the region separating the HST and Gaia stars used in our modelling. The black circles and vertical error bars feature the measured proper motion dispersion and respective 1σ uncertainty, calculated with the recipe from van der Marel & Anderson (2010, appendix A), in 10 logarithmically spaced radial bins. The horizontal error bars considered the 1σ radial quantization noise. The plot is originally from Vitral et al. 2023 and highlights the need for a very concentrated central dark mass in M4.

When removing a high-velocity star from the cluster center, the same mass excess is found, but more extended (∼0.034 pc ≈ 7000 au ). Using Monte Carlo N-body models of M4 to interpret the second outcome, we still found that our excess mass is not sufficiently extended to be confidently associated with a dark population of remnants. Although not a definitive proof of the existence of an IMBH (for instance, data incompleteness in the center could still affect our conclusions), this result is one of the best clues to the existence of IMBHs in globular clusters in our Milky Way.